0. Introduction

1. 재귀 알고리즘

이번에는 재귀 알고리즘에 대해 알아보겠다.

여기서 재귀란 **어떠한 이벤트에서 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의되는 경우**로서, recursion 이라 합니다.

이 관점에서 자연수를 재귀적 관점에서 다음과 같이 정의할 수 있다.

‘1은 자연수이고, 자연수의 바로 다음 수도 자연수다.’

무한히 존재하는 자연수를 재귀적 정의(recursive definition) 를 사용하여 간단히 정의했다.

이처럼 재귀 를 사용하며 프로그램을 간결하고 효율성 좋게 작성할 수 있다.

대표적인 예로 factorial이 있다.

10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1

코드로는 다음과 같다.

1
2
3
4
5

> def factorial(n: int) -> int:
>   if n > 0:
>       return n * factorial(n-1)
>   else:
>       return 1

이렇게 자신과 똑같은 함수를 호출하는 걸 재귀 호출(recursive call) 이라 한다.

파이썬에서는 팩토리얼 값을 구하는 표준 라이브러리로 math 모듈에서 factorial() 함수를 제공한다. math.factorial(x)를 하면 정수 x의 팩토리얼 값을 제공한다.

1.1 직접 재귀와 간접 재귀

하지만, 이 재귀도 두 가지로 나눠지는데 직접(direct) 재귀 와 간접(indirect) 재귀 로 나눠진다. 직접 재귀는 자신과 똑같은 함수를 반복해서호출하는 방식이며, 간접 재귀는 자신이 아닌 다른 함수를 호출하지만 이 다른 함수를 통해서 자신을 다시 호출하는 함수다. 아래 이미지를 참고하자.

image

1.2 유클리드 호제법(Euclidean algorithum)

재귀 알고리즘을 통해서 최대 공약수(GCD, Greater Common Divisor)를 재귀적으로 구하는 방법도 있다.

두 정수 x와 y의 최대 공약수를 구하는 함수를 gcd(x, y)라고 할 때, 최대 공약수는 다음과 같이 구별할 수 있다.

y가 0이면 x 이고, y가 0이 아니면 gcd(y, x % y)이다. 이 알고리즘을 유클리드 호제법이라 한다.

파이썬에서는 최대 공약수를 구하는 표준 라이브러리로 math module에서 gcd() 함수를 제공한다. math.gcd(a, b)는 a와 b의 최대 공약수를 반환한다.

2. 재귀 알고리즘 분석

2.1 재귀 알고리즘의 2가지 분석 방법

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

> def recure(n:int) -> int:
> """순수한 재귀 함수 구현"""

> if n > 0:
>   recur(n-1)
>   print(n)
>   recur(n-2)

> x = int(input('정숫값을 입력하세요. : '))

# 예를 들어 3을 입력했다고 하자.
> recure(x)

1
2
3
1

이처럼 함수 안에서 재귀 호출을 2번 이상하는 함수를 순수한(genuinely) 재귀 라고 하는데, 이 함수를 아래 2가지 방법으로 분석해보겠다.

하향식 방법(top-down) 방법과 상향식(bottom-up) 방법으로 분석하는 방법이다.

‘하향식 방법’에 대해 먼저 이야기 해보자.

**하향식 방법**이란 아래 이미지처럼 함수의 제일 첫 번째 호출부터 시작하여 계단식으로 자세히 조사해 나가는 방법 을 말한다.

image

이렇게 같은 함수를 여러 번 호출할 수 있으므로, 하향식 방법은 결코 효율적인 방법이 아니다.

다음으로 ‘상향식 방법’으로 분석해보자.

위에 recure 함수를 예로 들어 분석하자면 다음 이미지와 같다.

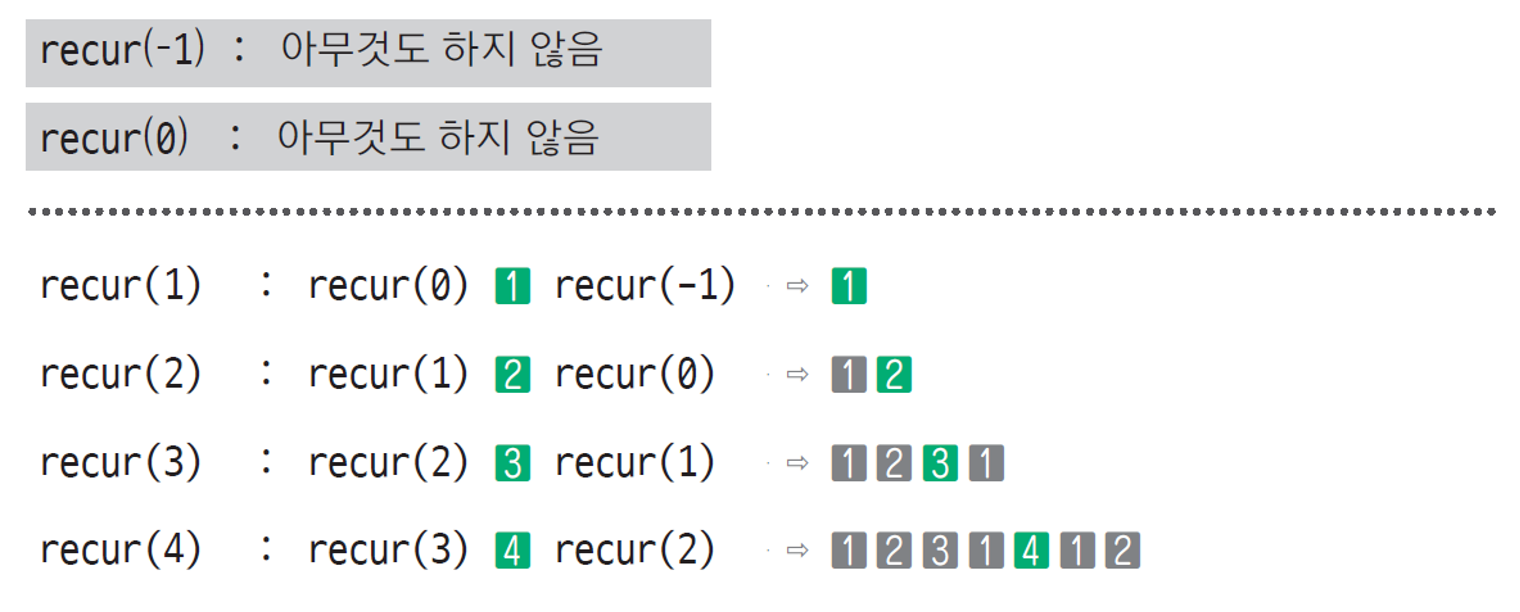
image

어디가 제일 바닥인지 알고, 이 밑에서부터 최초 호출 방향인 위로 접근하는 방법이다.

2.2 재귀 알고리즘의 비재귀적 표현

재귀 알고리즘을 재귀적 표현 없이 구현하기 위해서는 2가지 방법이 있다.

꼬리 재귀(tail recursion)를 제거하든가 또는 완전히 재귀를 제거하든가 이다.

2.2.1 꼬리 재귀 제거

꼬리 재귀를 제거하는건 끝 부분의 재귀를 제거하는 것이다.

recur(n-2)의 의미는 n의 값을 (n-2)로 업데이트하고, 시작 지점으로 돌아간다는 의미다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

> def recur(n: int) -> int
>    """꼬리 부분을 제거했기 때문에, while문을 사용"""
>   while n > 0:
>       recur(n-1)
>       print(n)
>       n = n - 2

> recur(5)

1
2
3
1
4
1
2
5
1
2
3
1

만약 while문으로 하지 않고, 그대로 if 문을 사용했을 경우 결과는 다음과 같다.

1
2
3
4
5

1
2
3
4
5

꼬리 부분을 제거하고, if 문을 유지했기 때문에 n = n - 2 로, n이 재할당되어도 반복되지 않았기 때문이다.

즉, 재귀함수의 꼬리 재귀를 제거하기 위해서는 if 문에서 while 문으로 바꿔야 한다는 걸 알 수 있다.

2.2.2 완전히 재귀를 제거

그러면 다음으로 완전히 재귀를 제거 해보자.

여기서 문제점이 있다.

앞 부분에 있는 recur(n-1) 을 꼬리 재귀를 제거했듯이 동일하게 간단히 제거할 수 없다. 그렇게 하면 n이 바로 출력되기 때문이다. n은 별도로 저장되었다가 나중에 출력되어야 한다.

이를 해결하기 위해서 stack data structure를 사용한다.

이전에 학습했던 method로는 pop(), push(), is_empty() 다.

여기서 직접 구현해보지 않겠다.

다음 이미지를 참고하여 구현해보자.

image

3. 하노이의 탑(Towers of Hanoi)

주어진 조건들은 다음과 같다.

  • 총 3개의 기둥이 있다.
  • 3개의 기둥 중 첫 번째 기둥에 n개의 원반이 있다.
  • 이 원반은 아래로 내려갈수록 면적이 커진다.

위 조건들을 바탕으로, 다음과 같은 규칙을 준수하면서 최소 이동 횟수 를 구하는 문제다.

  • 한 번에 한 개의 원반만 이동할 수 있다.
  • 큰 원반은 작은 원반 위에 쌓을 수 없다.

image

3개의 원반을 이동시킨다고 할 때, 다음과 같이 흘러간다.

image

recur과 동일하게 재귀함수 2개와 print 출력문 1개의 구성과 순서가 동일하다.

4. 8퀸 문제(8-Queen problem)

8퀸 문제는 다음과 같다.

64칸(8 x 8) 안에서 8개의 퀸이 서로 공격하여 잡을 수 없도록 배치하기

결론부터 말하자면 92가지 해결 방법이 나온다고 한다.

퀸을 배치할 수 있는 경우의 수는 64 x 63 x 62 x …. x 57 = 178,462,987,637,760 이다. 이를 8퀸 문제의 조건에 만족하는지 알아보는 건 비현실적이다.

그래서 먼저 이 문제에 숨겨진 규칙을 찾아보자.

  • 퀸은 같은 열에 있는 다른 퀸을 공격할 수 있으므로, 첫 번째 규칙, 각 열에 퀸을 1개만 배치한다.
  • 또한, 퀸은 같은 행에 있든 다른 퀸을 공격할 수 있으므로, 두 번째 규칙, 각 행에 퀸을 1개만 배치한다.

첫 번째 규칙을 적용하면 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 = 16,777,216 가지로 줄어든다.

여기서 두 번째 규칙을 적용하면 더 줄어든다는 건 계산해보지 않아도 알 수 있다.

분기 작업과 한정 작업을 합친 분기 한정법(branching and bounding method)을 통해서 접근한다.

- 분기(branching) 작업: 가지가 뻗어 나가듯이 배치 조합을 열거하는 방법

- 위에 하노이 탑이나 8퀸 문제처럼 큰 문제를 작은 문제로 분할하고, 작은 문제 풀이법을 결합하여 전체 풀이법을 얻는 방법을 **_분할 해결법(divide and conquer)_**  이라 한다. 이 때 주의할 점은 문제를 분할할 때, 작은 문제 풀이법에서 원래의 문제 풀이법을 쉽게 도출할 수 있도록 설계해야 한다.

- 한정 작업(bounding): 필요한 조합을 열거하지 않는 방법

Reference